最近各大 IT 企业的实习招聘都已如火如荼的开展，笔者本着“广撒网”的战略投了很多家公司的简历。现在不少知名IT公司（例如阿里、华为、美团）的笔试都已经转移到了线上来进行。笔者于昨晚参加了美团的在线笔试，相比于之前阿里和华为的笔试，美团的考查范围更广，难度也稍微高一些（会问很多计算机领域的基础知识，计网、操作系统、数据结构、算法甚至数据库都有涉及）。闲话不多说，我们接下来就一起看一下美团的两道编程题：

【笔者原创，仅供参考，若有纰漏，欢迎指正】

第一题 字符串距离

问题描述：

给定两个字符串 S 和 T，设 |S| 和 |T| 分别表示 S 和 T 的长度，保证 S 和 T 只包含两种字符a和b，并且 1 <= |T| <= |S| <= N，【N是一个不是很大的整数，笔者忘了具体的数据范围（逃】。定义两个等长字符串的距离为相应位置的不同字符个数的和，例如”abb”和”bab”的距离是 2（第一个字符、第二个字符不同）。两个不等长字符串 S 和 T，对于 S 字符串，它和 T 一样长的连续子串总共有 |S| – |T| + 1 个，这些连续子串和 T 的距离之和就是 S 和 T 的距离，例如“abba”和“ab”，考察 abba 的所有长度为 2 的连续子串，有 ab bb ba，它们和 ab 的距离分别为 0 1 2，故答案为 0+1+2=3。现在给定 S 和 T，求它们的距离。

输入格式：

共两行，第一行是 S，第二行是 T。

输出格式：

一个整数，代表 S 和 T 的距离。

解：

最暴力的做法，两层 for 循环，O(n²)，C/C++（时限 2s）能过 70%， Java（时限 4s）能过 90%。。。

优化一下，我们转化思路，以T中的每一个字符对最终结果的贡献度来看这道题。下面我们设 S=aaabbb，T=babb，则可以用下图中的方法来计算答案：

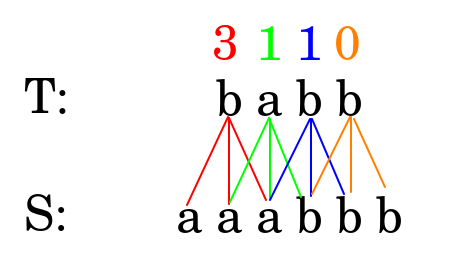
看！如果我们能在 O(1) 的时间内得出T中每个字符的“贡献度”，那么整个算法将是 O(n) 的（只需要遍历一遍 T 即可）！根据这个思路，我们首先形式化的定义一下“贡献度”：设 w=|S|-|T|+1，则 T 中第 i 个字符（i=0…|T|-1）的贡献度 F(i)=S[i…i+w) 这个子串里所有和 T[i] 不同的字符数目之和。仔细观察 F(i) 的定义，我们发现，问题的关键变成了快速地求出串 S 中某一特定连续子串中包含某种字符的数目。只要我们能在不多于 O(n) 的时间内求出这一数目，我们就可以在线性时间内得到整个问题的解。

那么如何求出串 S 中某一特定连续子串中包含某种字符的数目呢？相信聪明的读者已经发现，使用动态规划（DP）的思想，可以通过线性时间内的预处理得到这个数据。我们定义两个数组 a[i] 和 b[i]，分别表示 S 串长度为 i 的前缀含有 a 和含有 b 的个数。则可以得到：

根据这个递推规则我们就可以在 O(n) 时间内通过对 S 的预处理得到 a[] 和 b[]，并且在常数时间内通过计算 a[i+w] – a[i] 得到 S[i…i+w) 中字符 a 的数目（b 同理）。到此问题已解决，我们得到了时间复杂度为 O(n) 的算法，附上代码：

#include <iostream>
#include <string>
#include <cstring>
#include <vector>
using namespace std;

const int MAXN = 100010;

int main()
{
    string s, t;
    cin >> s >> t;
    long long int ans = 0;
    long long int w = s.length() - t.length() + 1;
    long long int a[MAXN], b[MAXN];
    memset(a, 0, sizeof(a));
    memset(b, 0, sizeof(b));
    a[0] = b[0] = 0;
    for (int i = 0; i < s.length(); ++i)
    {
        if (s[i] == 'a')
        {
            a[i + 1] = a[i] + 1;
            b[i + 1] = b[i];
        }
        else
        {
            a[i + 1] = a[i];
            b[i + 1] = b[i] + 1;
        }
    }
    for (int i = 0; i < t.length(); ++i)
    {
        if (t[i] == 'a')
            ans += b[i + w] - b[i];
        else
            ans += a[i + w] - a[i];
    }
    cout << ans << endl;
    return 0;
}

第二题 最小整数

问题描述：

给定一串数字字符，求使用这些数字字符拼不出来的最小整数。

输入格式：

一串数字字符

输出格式：

一个整数

样例输入 1：

123456789

样例输出 1：

10

样例输入 2：

55666777788

样例输出 2：

1

解：

仔细研究一些样例之后，我们不难找到如下规律：按照 0987654321 的顺序寻找给定个数最少的那个数字字符，如果最少的个数对应多个数字字符，那就应该让这个数字字符尽可能靠近上述顺序的右侧，不妨设这样找到的数字字符是 c（c = '0'…'9'），它的个数是 F[c]（0 <= F[c] <= N，N 为给定串长度上限）。则可以分为两种情况：

1. c 是 '0'，这代表 '1'…'9' 都至少有一个，并且 F[0] 是 F[0…9] 之中最小的，那么显然此时最小组不成的整数是“1后面加上 F[0]+1 个 0 组成的整数”。
2. c 不是'0'，这代表 '1'…'9' 中至少缺少一种数字字符（且 c 就是缺少的那些数字字符中最小的那个），那么显然此时最小组不成的整数是“F[c]+1 个 c 组成的整数”。

由此，可以写出解题代码如下：

#include <iostream>
#include <cstring>
using namespace std;

int main()
{
    int F[10];
    char t;
    memset(F, 0, sizeof(F));
    while (cin >> t)
    {
        ++F[t - '0'];
    }
    int c = 0;
    for (int i = 9; i >= 1; --i)
    {
        if (F[i] <= F[c])
            c = i;
    }
    if (c == 0)
    {
        cout << 1;
        for (int i = 0; i < F[c] + 1; ++i)
            cout << 0;
    }
    else
    {
        for (int i = 0; i < F[c] + 1; ++i)
            cout << c;
    }
    cout << endl;
    return 0;
}